| [ 組合せ最適化問題とそのアプローチ 北海道のOR より ] |
1.はじめに
一説には石油資源はほぼ70年以内には底をつくことになるとも言われている。このよ
うに、今後の社会システムにおいては限られた資源を有効に利用し最善の策を練るとい
うことが多くの場面で必要不可欠とならざるを得ない。すなわち、限られた制約のもと、
最善の策とは何かという問題へのアプローチが今後重要な課題となってくる。これらの
問題は最適化の問題と呼ばれる。その起源は人類の活動とともに始まったともいえ、こ
れらの問題は日常生活でも、たとえば、費用や時間の使い方、行動の計画や決定と
いったことなど絶えずわれわれの関心事となり、また悩みの種ともなっている。限られた
時間や財産を最大限有効に利用して、なるべく大きな満足を得たい（幸せになりたい）と
は、誰しもが常に望んでいることであろう。つまり最適化はわれわれにとって極めて日常
的でありかつ普遍的な問題である。今日言うような最適化問題が明確に意識され、数理
的にまとまった体系を形作るとともに、広範な応用分野が開拓されだしたのは、1940年
代後半にオペレーションズ・リサーチの研究が始まったころであるとみてよい。そして、
1950年代後半にコンピュータが実用化されるとともに、最適化の研究は飛躍発展を遂
げた。ところが、一概に最適化問題といっても幅が広く、過去の研究によって現在容易
に解けるものから、未だに計算困難なものまでバリエーションに富んでいる。
ここでは対象が組合せ的条件のもとでの最適化について述べたい。これを一般に組
合せ最適化問題と呼び、この問題の多くは厳密な答えを求めようとすると非常に厄介な
代物でもある。しかし、多くの分野で広範囲に応用されてもいる利用価値の高いもので
もある。その応用の一つとして配送計画の問題がある。これは最短距離あるいは最小
な時間でまわるルートを求める問題であり、配送コストという経済面でのメリットのみなら
ず、近年大きな問題となっている大気汚染や騒音などの環境問題、交通渋滞などの社
会問題への寄与ともなる。また、製造業においてはガラス、鉄、プラスチックの効率的な
裁断を行うために、この組合せ最適化の技法が利用されている。その他、生産スケジュ
ールの問題、配置の問題など多くの分野で利用され、限られた資源のもと少しでも生産
性や利益の追求が計られている。これらの問題は、すべての可能な組合せを列挙して
その中で最良な物を答えとすれば解けるわけであるから、数学的にはナンセンスな問題
のようである。しかし、その組合せの数は問題のサイズが大きくなるにしたがってあまり
にも大きくなる。たとえば、配送計画の一つのモデルでは30の都市数を回る最善のルー
トを求めるのに2000兆年以上の時間を要し、実質的には計算困難な問題となってしま
う。そこで、最良な値に近い答えで代替する戦略がとられるわけであるが、このアプロー
チとして自然界にアナロジーを持つことを特色とするメタヒューリスティックによる研究が
行われている。以下では具体的に組合せ最適化問題とその特性、およびそのアプロー
チであるメタヒューリスティックの手法について紹介しよう。
2.組合せ最適化問題
組合せ問題とは物事の組合せや順序などをうまく決めたいなど、実社会の様々な場面
で遭遇する問題であり、各種の形態の問題がある。その代表的問題といえば、何といっ
ても巡回セールスマン問題であろう。この章では代表格である巡回セールスマン問題に
ついて述べ、その中で組合せ最適化問題の特性を示したい。また、定められた形と面
積をもつ工場へ必要な機械類などの施設をどこにどう置くかの配置問題に利用される。
この問題においても巡回セールスマン問題同様その組合せ数は問題のサイズに対して
指数関数的に増大するため実質的には計算不可能である。
2.1 巡回セールスマン問題
巡回セールスマン問題(5)は、何ヶ所かの都市とその都市間の距離が与えられたとき、
すべての都市を巡り、元に戻る最短の道順を求める問題である。したがって、すべての
可能な道順を列挙してその中で最良な巡回路を見つければ解けるわけであるから、あ
まりにも単純でナンセンスな問題と思われるだろう。ところが、このナンセンスな問題が
計算機でも解けない難物中の難物なのである。もちろん、4都市なら高々6通りの道順し
かないので、その中で最短な順回路が答えであり、誰でも簡単に解ける問題である。と
ころが、その都市数が増えていくと道順の数がどうなるかが、この問題のネックとなるの
である。その道順の数は、都市数が n とすれば、出発点から次の都市への行き方は
(n - 1)通りであり、さらに、その都市から次の都市への行き方は(n - 2)と考えれば、
(n - 1)(n - 2)・・・2・1 通り( (n - 1)! 通り）となる。これはスターリングの公式
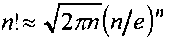によりほぼ nn 通りと表すことができ、都市数の増加により指数関数的にすべての可能
な道順の数が増加することがわかり、これを組合せ的爆発とよぶ。たとえば、100MIPS
ぐらいの計算機（1秒間に10万回の基本演算を行う）で20都市の問題を行うと、700年ぐ
らいの計算時間を要し、30都市以上にいたってはもはや数兆億年という天文学的計算
時間を要してしまう。また、これらの問題はいかに計算機のスピードが高速になろうが、
その計算時間は雀の涙ほどしか改善されない。というか必要とする計算時間は残念な
がら天文学的値のままである。しかし、多くの研究、工夫がなされてきており、巡回セー
ルスマン問題に対する性質を利用してかなりの程度の問題を解けるようにもなってきて
いるのも事実である。
巡回セールスマン問題の応用として電子部品のプリント基盤への自動装着システムに
おける実装順序に利用されている。他にも問題の名前からお分かりの通り、配送計画
への利用がある。さらに、この応用で巡回セールスマン問題を複雑化した、すなわち、
輸送トラックの容量に合わせて数度配送センターへ戻ることを考慮したビークルルーティ
ング問題などのより現実化した問題への適用なども考えられている。
2.2 分割問題
これはあるシステム全体を構成する多くの部分要素をひとまとめに分割し、まとめたも
の同士（集合）の組合せを構成する。このとき、分割された集合同士のつながりの度合
などの評価値を最良にする分割の組合せを考える問題である。その応用の最たるもの
は配線総量を最小になるように回線素子を分割配置する超大規模集積回路（VLSI）設
計の問題があげられる。また、定められた形と面積をもつ工場へ必要な機械類などの
施設をどこにどう置くかの配置問題に利用される。この問題においても巡回セールスマ
ン問題同様その組合せ数は問題のサイズに対して指数関数的に増大するため実質的
には計算不可能である。
2.3 スケジューリング問題
スケジューリング問題は生産加工にあたって、どの生産設備でいつ、いかなる作業を
行うかという問題であり、その基本的問題としてジョブ・ショップスケジューリングの問題
がある。n 台の異なる機械からなる工場で m 個の違った製品を加工する問題について
製品製作の仕事を時間軸上に割り付けることが問題となる。この問題も一般的な解決
は容易ではなく、n 台の機械によって m 個のジョブを処理するには(m !)n 通りの方法が
あり組合せ的爆発を起こしてしまう。
3.メタ戦略によるアプローチ
巡回セールスマン問題に代表される組合せ最適化問題の多くはいわゆるNP困難な問
題のクラスに属し、問題のサイズに対して計算時間が指数関数的に増大する。このため
実用的な時間内で精密な解を求めることは困難であり、通常、近似的な値をもつ解に
よって代替する戦略が取られる。すなわち、巡回セールスマン問題では、一番最短な巡
回路を求めることが困難なので、それにできるだけ近い距離の順回路を求めることであ
るが、通常、実際的にもこの程度の値で十分問題はないであろう。このため、多くの近
似解法が提案され実用化が計られている。本章ではその中で、最近多くの成果をあげ
ているパラダイムであるメタヒューリスティックを紹介し、その効果について論じたい。
メタヒューリスティックは従来の組合わせ最適化問題を解くための種々の戦略を有機
的に結合させたり、あるいは反復させたものであり、従来の近似解法を超えたパラダイ
ムとして注目を浴びている。このとき、各手法においていくつかのパラメータを制御する
ことによって、様々な戦略を構成できる。すなわち、メタヒューリスティックとはヒューリス
ティックにパラメータを追加し、そこで生まれた自由度を用いて問題を巧く解くテクニック
であり、それを工夫することによって、組合わせ最適化問題に対する実用的なツールと
なり得る。
このように、メタヒューリスティックの実用化にはパラメータの適正化が不可欠であるが
このパラメータの適正値は通常、系統的な数値実験によって得られる。
ここでは、Local search法、Tabu Search法、Simulated Annealing法などのメタヒューリ
スティック(4)を示す。多くのメタヒューリスティックは自然界にアナロジーを持つことを一つ
の特色とする（それが必要条件ではない）。Tabu Search法は人間の記憶過程にアナロ
ジーを持つ。すなわち、最近記憶した情報をもとに、再び、無駄な同一過程を繰返さない
戦略からなる。Simulated Annealing法 は物理現象の焼き鈍しのアナロジーから構成さ
れる。すなわち、高い温度から低い温度へと十分にゆっくりと冷却するとき、結晶構造が
最大化する現象を組合わせ問題の最適化問題に置き換えたものである。また、生物の
進化の現象を取入れた遺伝アルゴリズム、および蟻のコロニー形成を模倣したアントシ
ステムアルゴリズムもこの範疇に属するものである。
3.1 Local Seach法
この方法は山登りに例えれば、現在の場所から限られた視野の範囲で決して下がる
ことなく、高いほう、高いほうと進んでいき、もはや上れなくなった段階でその場所を答え
とする方法である。しかしこの上れなくなった場所が多くの山の中での最高峰（求めたい
厳密解）ではなく、せいぜい丘（局所解）程度であろう。
3.2 Tabu Search法
Local Search法だと探索の過程で一度求めた解に再び戻ってくるサイクリングという現
象を起すことがある。これに対してTabu Search(2)はタブーリストといういう記憶域を設け
最近探索した解への進行を禁止する。すなわち、山登りの例でいえば、一度通った道は
覚えておき、再び通らないようにする戦略である。また、上る道が存在しなければ、勾配
の小さい下る道へ進むことも許されている。
3.3 Simulated Annealing法
Simulated Annealing法(3)は結晶構造が温度減少にともなって最大化する現象を最適
化問題の探索過程に適用したものである。山登りの例でいえば、道の探索に確率的要
素を導入し、より高い山へと上っていく方法である。すなわち、まず、さいころを転がし適
当に道を選択する。そして、それが上る道ならば進行するが、下る道ならば、その勾配
の程度によって、進行したりしなかったりしながら進んでいく。しかし、温度というパラメー
タによって最初のうちは下る勾配が大きくても受け入れる確立が高いが、だんだんと下
る道を拒絶する確率を高くするように制御していく。実に都合のよいことに、この方法は
理論的に最適解に収束することが証明されている。しかし、残念ながらその収束に要す
る時間は指数的オーダーであり、その理論的特性を利用することは不可能であろう。
実際には実用時間内で計算され収束された値を用いている。
3.4 遺伝アルゴリズム
遺伝アルゴリズムは最近、特に多くの分野で行われている研究の一つである。遺伝子
の進化にアイディアを取り、増殖、突然変異および淘汰などに類似したプロセスを組み
入れた確率的探索法である。Simulated Annealing法と同様確率的要素が導入されるが
大きく異なる点として遺伝子という解に対応する要素からなる集合によってプロセスが
進行する。まず、ある適応度で集団からなる遺伝子に対して淘汰を行う。次に、任意の
2つの遺伝子からその形質を受継ぐ２つの子遺伝子を生成していく（交叉）、さらにある
確率で突然変異をかけ次の世代とする。この進化過程により優良な遺伝子（解）を探索
するわけである。
3.5 アントシステムアルゴリズム
最近手がけている研究でアントシステムアルゴリズム(1)がある。その基本的考え方は
複数のアントがランダムに進行するとき、短い距離の２点間に多くのフェロモンが付着す
ることにより最終的に短距離間のアントの行進が完成するというアナロジーである。具体
的にはフェロモンという大域的情報を介して、複数のアントというエージェントがそのフェ
ロモン情報と次の都市への距離情報によって道を選択していくというアルゴリズムである。
4.おわりに
副題に計算機で解けない問題とはったりをかましたが、むしろ計算困難といったほうが
近いであろう。このような計算困難な組合せ最適化の問題はここで紹介しきれないほど
他にも数多くある。我々の身近な世界の中にもこのような問題はあり、研究対象としたな
らば面白い問題となるものもあるであろう。また、組合せ問題に対する代表的アプロー
チの概略を述べが、それらのアプローチに対しておおくは何らかの戦略を組込んだり、
ハイブリッド化することによって改良を行っている。しかし、基本的構成のみのアルゴリ
ズムについて検討すると、Local Search法はこの手の近似解法の基本であり、単純な構
成であるがよい解は求まらない。Tabu Search法は短時間内で優良な解を探索するの
に優れている。Simulated Annealing法は研究室で扱った問題に限れば、一番良好な値
を示す傾向が高い。遺伝アルゴリズムは大域的探索は優れているが局所的探索に劣る
ところがある。したがって、Tabu Searchなどとのハイブリッド化が有効であるとのこと。
アントシステムアルゴリズムは最近研究が始められた段階であり今後が期待される。
この分野に関していえば、今後さらなる展開が予想され、また、新たなパラダイムを
もったアルゴリズムも提案されていくであろう。
参考文献
(1) Dorigo M., Maniezzo V. and Colorni A. : "The Ant System: Optimization by a colony
of cooperating agents", IEEE Transactions on Systems, Man and Cybernetics-Part B,
Vol.26, No.1, pp.1-26(1996).
(2) 加地, 大内 : Tabu Search法による無閉路有向グラフの最適系列分割問題の解法,
電学論ｃ, Vol.116-C, No.10, pp.1149-1157(1996).
(3) 加地、大内 : 系列分割問題に対する確率的複合移動によるSimulated Annealing法
の適用, 情報処理学会論文誌, Vol.38, No.12, pp.2411-2418(1997).
(4) 久保：離散構造とアルゴリズムⅣ（メタヒューリスティックス）、近代科学社(1995).
(5) 山本、久保：巡回セールスマン問題への招待、朝倉書店(1997).
|